An alternative bezier arrow to the regular grid-bezier. Apart from a cool gradient it has the advantages of: exact width, exact start/end points and axis alignment.

About two weeks ago I got frustrated with the bezierGrob function in the grid package. The lwd parameter is interpreted differently depending on device, the arrow at the end does not follow the line but is perpendicular (probably following the spline control), and the line parameter makes it difficult to control exactly where the line starts/ends. Thus I decided to make my own fancy line with an arrow at the end – at the time I thought: How hard can it be? In retrospect, I wish I never thought of the thing… This article is about the painful process of creating of an alternative to the bezierGrob.

The end result

Based upon this article I have created two functions for generating these arrows, you can find them in my Gmisc-package, the bezierArrowSmpl and bezierArrowSmplGradient functions. Both functions should be fully documented, although the second one with the gradient is still somewhat of a beta as there are more features that I’m thinking of adding in the future. The first basic arrow is actually just a polygonGrob while the gradient arrow builds upon this one with a gradient layer on top – all merged into a gList grob. Grob stands for graphical object as defined by the grid-package. One day I also hope to convert these into proper grobs according to Paul Murrel’s grob-concept, but after skimming through the manual I quickly decided that it will have to wait for a while… right now I’m just happy that it works after a lot of debugging.

The process

So I started out with just generating some settings so that it would be easier to convert into a function later on.

library(grid)
default.units <- "npc"
end_points <- list(start = list(x = 0.2, y = 0.2), end = list(x = 0.8, y = 0.6))
spline_ctrl <- list(start = list(x = 0.5, y = 0.2), end = list(x = 0.5, y = 0.8))
spline_ctrl$start$length <- sqrt((spline_ctrl$start$x - end_points$start$x)^2 + 
    (spline_ctrl$start$y - end_points$start$y)^2)
spline_ctrl$end$length <- sqrt((spline_ctrl$end$x - end_points$end$x)^2 + (spline_ctrl$end$y - 
    end_points$end$y)^2)
width <- unit(0.05, "npc")

arrow <- list(base = unit(0.1, "npc"), length = unit(0.1, "npc"))

gradient <- list(type = "triangle", decrease_prop = 0.4, start_prop = 0.25, 
    clr_prop = 0.7, line_width = unit(8, "pt"), clr = "#2F4F2F")

clr <- "#000000"

So by calling the bezierGrob function we get a nice curvy line.

plot.new()

bz_grob <- bezierGrob(x = c(end_points$start$x, spline_ctrl$start$x, spline_ctrl$end$x, 
    end_points$end$x), y = c(end_points$start$y, spline_ctrl$start$y, spline_ctrl$end$y, 
    end_points$end$y), default.units = "npc", gp = gpar(lwd = 2, col = grey(0.1)))
grid.draw(bz_grob)

Next we get the actual points of the bezier curve. We also want the viewport's values so we need to convert it all the values into npc. On top of this I prefer to remove the unit as this complicates the calculations.

bp <- bezierPoints(bz_grob)
bp$y <- convertY(bp$y, unitTo = default.units, valueOnly = TRUE)
bp$x <- convertX(bp$x, unitTo = default.units, valueOnly = TRUE)
getLength <- function(x, y) {
    m <- rbind(y, x)
    # Map the change between coordinates
    m <- m[, 2:ncol(m)] - m[, 1:(ncol(m) - 1)]
    # Set first element to 0 length
    m <- cbind(c(0, 0), m)
    # The old sqrt(a^2+b^2) formula
    return(sqrt(colSums(m^2)))
}
bp$lengths <- getLength(bp$x, bp$y)

Lets see if we can plot a polygon using the points. As you can see the width isn't really as expected since the shift is only vertical.

pg <- polygonGrob(x = c(bp$x, rev(bp$x)), y = c(bp$y + 0.1, rev(bp$y - 0.1)), 
    gp = gpar(fill = clr))
grid.draw(pg)

Cutting the curve at the arrow

We want to cut the bezier curve so that we get an arrow of a certain length. This turned out to be a little tricky as I needed to find the point that is the closes corresponding one to my desired length.

getBestMatchForArrowLengthAlongCurve <- function(bp, arrow_length) {
    if (class(arrow_length) == "unit") 
        arrow_length <- convertUnit(arrow_length, unitTo = default.units, valueOnly = TRUE)
    no_points <- length(bp$y)
    end_point <- list(x = bp$x[no_points], y = bp$y[no_points])
    # Just a guess
    best_point <- round(no_points * 0.9)
    for (i in 1:no_points) {
        lb <- sqrt((bp$x[best_point] - end_point$x)^2 + (bp$y[best_point] - 
            end_point$y)^2)
        l_plus <- sqrt((bp$x[best_point + 1] - end_point$x)^2 + (bp$y[best_point + 
            1] - end_point$y)^2)
        l_minus <- sqrt((bp$x[best_point - 1] - end_point$x)^2 + (bp$y[best_point - 
            1] - end_point$y)^2)
        best_diff <- abs(lb - arrow_length)
        plus_diff <- abs(l_plus - arrow_length)
        minus_diff <- abs(l_minus - arrow_length)

        if (best_diff < plus_diff && best_diff < minus_diff) 
            return(best_point) else if (plus_diff < minus_diff) 
            best_point <- best_point + 1 else best_point <- best_point - 1

        # Reached the end without finding an optimal point
        if (best_point == 1 || best_point == no_points) {
            break
        }
    }

    warning("Could not find the optimal point along the line", " that would correspond to the desired arrow length")
    return(best_point)
}

bp$cut_point <- getBestMatchForArrowLengthAlongCurve(bp, arrow$length)

# Set the arrow details according to this new information
arrow$x <- end_points$end$x - bp$x[bp$cut_point]
arrow$y <- end_points$end$y - bp$y[bp$cut_point]
arrow$length <- sqrt(arrow$x^2 + arrow$y^2)

Now lets see where that gets us.

end_points$end$new_x <- bp$x[bp$cut_point]
end_points$end$new_y <- bp$y[bp$cut_point]

new_bz_grob1 <- bezierGrob(x = c(end_points$start$x, spline_ctrl$start$x, spline_ctrl$end$x, 
    end_points$end$new_x), y = c(end_points$start$y, spline_ctrl$start$y, spline_ctrl$end$y, 
    end_points$end$new_y), default.units = default.units, gp = gpar(lwd = 4, 
    col = "blue"))

plot.new()
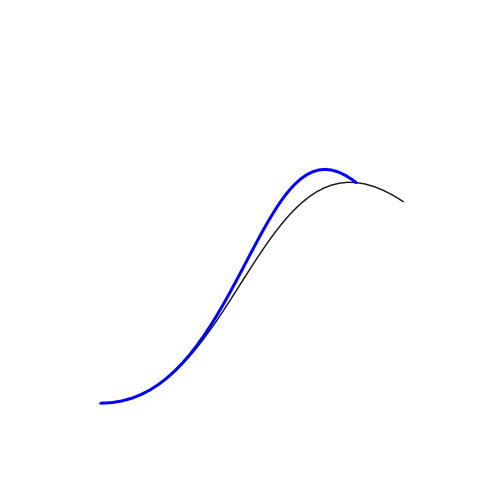
grid.draw(bz_grob)
grid.draw(new_bz_grob1)

It seems rather obvious that we can't use the same spline controls. The best solution is to adjust the spline control so that it matches the direction of the arrow. It's not perfect but since I'm not familiar with the bezier generating code (the xspline function), it will have to do.

getBezierAdjustedForArrow <- function(end_points, spline_ctrl, arrow) {
    multiplier <- (spline_ctrl$end$length - arrow$length * 1.5)/arrow$length
    # Use the arrow's vector in the opposite direction as the nwew ctrl point
    spline_ctrl$end$new_x <- -arrow$x * multiplier + bp$x[bp$cut_point]
    spline_ctrl$end$new_y <- -arrow$y * multiplier + bp$y[bp$cut_point]

    simple_start_adjustment <- 1 - arrow$length/sum(bp$lengths)/3
    # Remove a fraction of the distance for the spline controles
    spline_ctrl$start$new_x <- end_points$start$x + (spline_ctrl$start$x - end_points$start$x) * 
        simple_start_adjustment
    spline_ctrl$start$new_y <- end_points$start$y + (spline_ctrl$start$y - end_points$start$y) * 
        simple_start_adjustment

    bezierGrob(x = c(end_points$start$x, spline_ctrl$start$new_x, spline_ctrl$end$new_x, 
        end_points$end$new_x), y = c(end_points$start$y, spline_ctrl$start$new_y, 
        spline_ctrl$end$new_y, end_points$end$new_y), default.units = default.units, 
        gp = gpar(lwd = 4, col = "orange"))
}

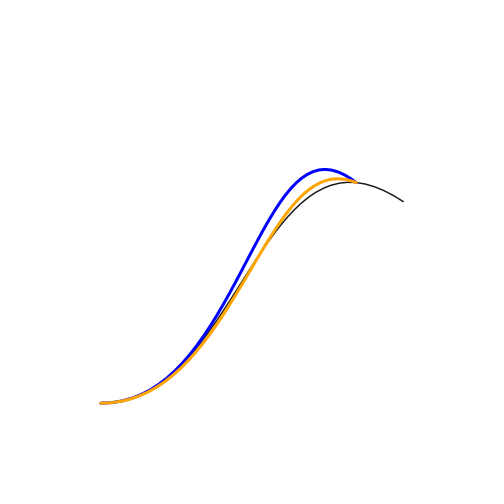
new_bz_grob2 <- getBezierAdjustedForArrow(end_points, spline_ctrl, arrow)

plot.new()
grid.draw(bz_grob)
grid.draw(new_bz_grob1)
grid.draw(new_bz_grob2)

The rectangle

Now let's kick of with the rectangle that we want. In this step we need to offset the lines by a certain amount. All those hours with linear algebra actually simplified it a little.

new_bp <- bezierPoints(new_bz_grob2)
new_bp$y <- convertY(new_bp$y, unitTo = default.units, valueOnly = TRUE)
new_bp$x <- convertX(new_bp$x, unitTo = default.units, valueOnly = TRUE)
getBzLength <- function(x, y) {
    m <- rbind(y, x)
    # Map the change between coordinates
    m <- m[, 2:ncol(m)] - m[, 1:(ncol(m) - 1)]
    # Set first element to 0 length
    m <- cbind(c(0, 0), m)
    # The old sqrt(a^2+b^2) formula
    return(sqrt(colSums(m^2)))
}
new_bp$lengths <- getBzLength(new_bp$x, new_bp$y)
# Add the arrow length to the last element
new_bp$lengths[length(new_bp$lengths)] <- new_bp$lengths[length(new_bp$lengths)] + 
    arrow$length


#' Checks the input
#'
#' @param x The x point of the vector
#' @param y The y point of the vector
#' @param x_origo The x origin if other than 0
#' @param y_origo The y origin if other than 0
#' @return list with the input variables checked and
#'  converted if necessary.
validateAndConvertVectorInputs <- function(x, y, x_origo = NA, y_origo = NA) {
    # Just som sanity input check
    if (class(y) != class(x)) 
        stop("The x and y point don't have the same class,", " should be either numeric or units.", 
            " Currently you have provided y=", class(y), " & x=", class(x))

    if (is.na(x_origo) != is.na(y_origo)) 
        stop("You mus specify both origo points!")

    if (is.na(x_origo)) {
        if ("unit" %in% class(y)) 
            y_origo <- x_origo <- unit(0, attr(y, "unit")) else x_origo <- y_origo <- 0
    }

    if (class(y_origo) != class(x_origo)) 
        stop("The x and y point for the origo point don't have the same class,", 
            " should be either numeric or units.", " Currently you have provided y=", 
            class(y), " & x=", class(x))

    if (class(y) != class(y_origo)) 
        stop("The angle won't make any sense if your x and y point", " doesn't have the same unit as the origo x and y point.", 
            " Currently you have provided point class=", class(y), " & origo class=", 
            class(x))

    return(list(y = y, x = x, y_origo = y_origo, x_origo = x_origo))
}

#' Gets an angle
#'
#' @param x The x point of the vector
#' @param y The y point of the vector
#' @param x_origo The x origin if other than 0
#' @param y_origo The y origin if other than 0
#' @return angle as defined by \code{\link{atan}}
getVectorAngle <- function(x, y, x_origo = NA, y_origo = NA) {
    v <- validateAndConvertVectorInputs(x = x, y = y, x_origo = x_origo, y_origo = y_origo)

    if (class(v$y) == "unit") {
        y_diff <- convertY(v$y - v$y_origo, unitTo = default.units, valueOnly = TRUE)
        x_diff <- convertX(v$x - v$x_origo, unitTo = default.units, valueOnly = TRUE)
    } else {
        y_diff <- v$y - v$y_origo
        x_diff <- v$x - v$x_origo
    }

    return(atan(y_diff/x_diff))
}

#' Rotates a width to match a vector
#'
#' @param x The x point of the vector
#' @param y The y point of the vector
#' @param x_origo The x origin if other than 0
#' @param y_origo The y origin if other than 0
#' @param width The width of the desired up & down vectors
#' @param perpendicular If the width is perpendicular to
#'  the provided vector the set this to true
#' @param prev_angle If you want an average from this and the
#'  previous angle then set this parameter to the previous
#'  angle
#'
#' @return list A list with up & down vectors of c(x, y) format
#'  and a angle element
rotateWidth <- function(x, y, x_origo = NA, y_origo = NA, width = 0, default.units = "npc", 
    perpendicular = TRUE, prev_angle = NA) {
    v <- validateAndConvertVectorInputs(x = x, y = y, x_origo = x_origo, y_origo = y_origo)
    angle <- getVectorAngle(x = x, y = y, x_origo = x_origo, y_origo = y_origo)
    working_angle <- mean(c(angle, prev_angle), na.rm = TRUE)

    rot_mtrx <- rbind(c(cos(working_angle), -sin(working_angle)), c(sin(working_angle), 
        cos(working_angle)))

    # We need to convert the width into a scalar before we can work with it
    if (class(width) == "unit") {
        w_unit <- attr(width, "unit")
        w_scalar <- convertUnit(width, unitTo = w_unit, valueOnly = TRUE)
    } else {
        w_scalar <- width
        w_unit <- default.units
    }

    if (perpendicular) 
        width_vector <- c(x = 0, y = w_scalar/2) else width_vector <- c(x = w_scalar/2, y = 0)

    up <- as.vector(rot_mtrx %*% width_vector)
    down <- -up

    # Convert back to units
    up <- unit(up, w_unit)
    down <- unit(down, w_unit)

    if ("unit" %in% class(v$x_origo)) {
        up <- up + unit.c(v$x_origo, v$y_origo)
        down <- down + unit.c(v$x_origo, v$y_origo)
    } else {
        up <- up + unit(c(v$x_origo, v$y_origo), default.units)
        down <- down + unit(c(v$x_origo, v$y_origo), default.units)
    }

    return(list(up = up, down = down, angle = angle))
}


getLines <- function(arrow, width, new_bp) {
    line_offset <- rotateWidth(x = arrow$x, y = arrow$y, width = width, perpendicular = TRUE)
    top <- list(x = unit.c(unit(new_bp$x, default.units) + line_offset$up[1]), 
        y = unit.c(unit(new_bp$y, default.units) + line_offset$up[2]))
    bottom <- list(x = unit.c(unit(new_bp$x, default.units) + line_offset$down[1]), 
        y = unit.c(unit(new_bp$y, default.units) + line_offset$down[2]))
    return(list(top = top, bottom = bottom))
}

line_offset <- rotateWidth(x = arrow$x, y = arrow$y, width = width, perpendicular = TRUE)

lines <- getLines(arrow, width, new_bp)
pg <- polygonGrob(x = unit.c(lines$top$x, rev(lines$bottom$x)), y = unit.c(lines$top$y, 
    rev(lines$bottom$y)), gp = gpar(col = NA, fill = clr))
plot.new()
grid.draw(pg)

Although this may look a little artistic, it causes some issues, the line width should be perpendicular to each node. To get this we need to recalculate each node. Although theoretically it is time consuming, graphs shouldn't be that sensitive to slow performance. There is probably a matrix short-cut, but then it would loose the width unit as the operations on a unit are limited. I also found it better to actually average the angle between the nodes.

getLines <- function(new_bp, arrow, width, default.units) {
    # This initiation is necessary due to the unit inflexibility
    up_down <- rotateWidth(x_origo = new_bp$x[1], y_origo = new_bp$y[1], x = new_bp$x[2], 
        y = new_bp$y[2], width = width, perpendicular = TRUE)
    lines <- list(top = list(x = up_down$up[1], y = up_down$up[2]), bottom = list(x = up_down$down[1], 
        y = up_down$down[2]))

    # Add the offset to the return variable
    addLineOffset <- function(x, y, lines, offset) {
        lines$top$x <- unit.c(lines$top$x, offset$up[1])
        lines$top$y <- unit.c(lines$top$y, offset$up[2])
        lines$bottom$x <- unit.c(lines$bottom$x, offset$down[1])
        lines$bottom$y <- unit.c(lines$bottom$y, offset$down[2])
        return(lines)
    }

    for (i in 2:(length(new_bp$x) - 1)) {
        up_down <- rotateWidth(x_origo = new_bp$x[i], y_origo = new_bp$y[i], 
            x = new_bp$x[i + 1], y = new_bp$y[i + 1], width = width, perpendicular = TRUE, 
            prev_angle = up_down$angle)
        lines <- addLineOffset(new_bp$x[i], new_bp$y[i], lines, up_down)
    }

    # For the last element use the arrow direction
    up_down <- rotateWidth(x = arrow$x + new_bp$x[i + 1], y = arrow$y + new_bp$y[i + 
        1], x_origo = new_bp$x[i + 1], y_origo = new_bp$y[i + 1], width = width, 
        perpendicular = TRUE)
    lines <- addLineOffset(new_bp$x[i + 1], new_bp$y[i + 1], lines, up_down)

    return(lines)
}

lines <- getLines(new_bp, arrow, width, default.units)

pg <- polygonGrob(x = unit.c(lines$top$x, rev(lines$bottom$x)), y = unit.c(lines$top$y, 
    rev(lines$bottom$y)), gp = gpar(col = NA, fill = clr))
plot.new()
grid.draw(pg)

Now lets see if we can get the left side to be vertical.

getLines <- function(new_bp, arrow, width, default.units, align_2_axis = TRUE) {
    # This initiation is necessary due to the unit inflexibility
    up_down <- rotateWidth(x_origo = new_bp$x[1], y_origo = new_bp$y[1], x = new_bp$x[2], 
        y = new_bp$y[2], width = width, perpendicular = TRUE)
    lines <- list(top = list(x = up_down$up[1], y = up_down$up[2]), bottom = list(x = up_down$down[1], 
        y = up_down$down[2]))

    # Add the offset to the return variable
    addLineOffset <- function(x, y, lines, offset) {
        lines$top$x <- unit.c(lines$top$x, offset$up[1])
        lines$top$y <- unit.c(lines$top$y, offset$up[2])
        lines$bottom$x <- unit.c(lines$bottom$x, offset$down[1])
        lines$bottom$y <- unit.c(lines$bottom$y, offset$down[2])
        return(lines)
    }

    for (i in 2:(length(new_bp$x) - 1)) {
        up_down <- rotateWidth(x_origo = new_bp$x[i], y_origo = new_bp$y[i], 
            x = new_bp$x[i + 1], y = new_bp$y[i + 1], width = width, perpendicular = TRUE)
        lines <- addLineOffset(new_bp$x[i], new_bp$y[i], lines, up_down)
    }

    # For the last element use the arrow direction
    up_down <- rotateWidth(x = arrow$x + new_bp$x[i + 1], y = arrow$y + new_bp$y[i + 
        1], x_origo = new_bp$x[i + 1], y_origo = new_bp$y[i + 1], width = width, 
        perpendicular = TRUE)
    lines <- addLineOffset(new_bp$x[i + 1], new_bp$y[i + 1], lines, up_down)


    # Start with the easy part, cutting off excess line
    shortenLine <- function(x, y, ref_x, ref_y, default.units, shorten_by_x = TRUE) {
        if ("unit" %in% class(x)) 
            x <- convertX(x, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(y)) 
            y <- convertY(y, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(ref_x)) 
            ref_x <- convertX(ref_x, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(ref_y)) 
            ref_y <- convertY(ref_y, unitTo = default.units, valueOnly = TRUE)

        if (shorten_by_x) 
            cut_point <- which(x < ref_x) + 1 else cut_point <- which(y < ref_y) + 1

        x <- unit(c(ref_x, x[cut_point:length(x)]), default.units)
        y <- unit(c(ref_y, y[cut_point:length(y)]), default.units)

        return(list(x = x, y = y))
    }


    # Adds the missing piece by generating another bezier curve for that
    # specific section
    extendLine <- function(x, y, ref_x, ref_y, default.units) {
        if ("unit" %in% class(x)) 
            x <- convertX(x, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(y)) 
            y <- convertY(y, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(ref_x)) 
            ref_x <- convertX(ref_x, unitTo = default.units, valueOnly = TRUE)
        if ("unit" %in% class(ref_y)) 
            ref_y <- convertY(ref_y, unitTo = default.units, valueOnly = TRUE)

        distanceX <- x[1] - ref_x
        distanceY <- y[1] - ref_y

        # Generate a grob for the remaining spline
        add_bg <- bezierGrob(x = c(x[1], x[1] + distanceX/2, x[1] + distanceX/2, 
            ref_x), y = c(y[1], y[1], y[1] + distanceY/2, ref_y))
        add_bg_pt <- bezierPoints(add_bg)
        add_x <- convertX(add_bg_pt$x, unitTo = default.units, valueOnly = TRUE)
        add_y <- convertY(add_bg_pt$y, unitTo = default.units, valueOnly = TRUE)
        x <- unit(c(add_x, x), default.units)
        y <- unit(c(add_y, y), default.units)
        return(list(x = x, y = y))
    }

    angle <- getVectorAngle(x_origo = new_bp$x[1], y_origo = new_bp$y[1], x = new_bp$x[2], 
        y = new_bp$y[2]) * 180/pi
    # If vertical
    if (angle < 45 && align_2_axis) {
        # Get the original points of interest
        org_offset <- rotateWidth(x_origo = new_bp$x[1], y_origo = new_bp$y[1], 
            x = new_bp$x[1] + new_bp$x[1], y = new_bp$y[1], width = width, perpendicular = TRUE)
        # Check if to or bottom line is the shorter one
        if (new_bp$y[2] - new_bp$y[1] > 0) {
            # Top is shorter
            lines$top <- shortenLine(x = lines$top$x, y = lines$top$y, ref_x = org_offset$up[1], 
                ref_y = org_offset$up[2], default.units = default.units, shorten_by_x = TRUE)
            lines$bottom <- extendLine(x = lines$bottom$x, y = lines$bottom$y, 
                ref_x = org_offset$down[1], ref_y = org_offset$down[2], default.units = default.units)
        } else {
            lines$bottom <- shortenLine(x = lines$bottom$x, y = lines$bottom$y, 
                ref_x = org_offset$down[1], ref_y = org_offset$down[2], default.units = default.units)
            lines$top <- extendLine(x = lines$top$x, y = lines$top$y, ref_x = org_offset$up[1], 
                ref_y = org_offset$up[2], default.units = default.units)
        }
    } else if (align_2_axis) {
        # Horizontal
    }
    return(lines)

}


lines <- getLines(new_bp = new_bp, arrow = arrow, width = width, default.units = default.units)

pg <- polygonGrob(x = unit.c(lines$top$x, rev(lines$bottom$x)), y = unit.c(lines$top$y, 
    rev(lines$bottom$y)), gp = gpar(col = NA, fill = clr))
plot.new()
grid.draw(pg)

It looks OK with the vertical althought there as the angle increases to 45 degrees I should probably change the bezier adding code. Now lets finally add the arrow.

getLinesWithArrow <- function(new_bp, arrow, end_points, width, default.units, 
    align_2_axis = TRUE) {
    lines <- getLines(new_bp = new_bp, arrow = arrow, width = width, default.units = default.units)

    tmp <- rotateWidth(x = arrow$x, y = arrow$y, width = arrow$base)
    arrow$up <- tmp$up
    arrow$down <- tmp$down
    lines$top$x <- unit.c(lines$top$x, lines$top$x[length(lines$top$x)] + arrow$up[1], 
        unit(end_points$end$x, default.units))
    lines$top$y <- unit.c(lines$top$y, lines$top$y[length(lines$top$y)] + arrow$up[2], 
        unit(end_points$end$y, default.units))
    lines$bottom$x <- unit.c(lines$bottom$x, lines$bottom$x[length(lines$bottom$x)] + 
        arrow$down[1])
    lines$bottom$y <- unit.c(lines$bottom$y, lines$bottom$y[length(lines$bottom$y)] + 
        arrow$down[2])

    return(lines)
}

lines <- getLinesWithArrow(new_bp = new_bp, arrow = arrow, end_points = end_points, 
    width = width, default.units = default.units)

pg <- polygonGrob(x = unit.c(lines$top$x, rev(lines$bottom$x)), y = unit.c(lines$top$y, 
    rev(lines$bottom$y)), gp = gpar(col = NA, fill = clr))
plot.new()
grid.draw(pg)

The damn gradient

Now to the really tricky part, adding a color gradient. I did have a lot of fun in this section although in the end the debugging was really tiresome. This section is more expanded in the bezierArrowSmplGradient function.

end_point <- which(cumsum(new_bp$lengths) >= sum(new_bp$lengths) * (gradient$start_prop + 
    gradient$decrease_prop))[1] - 2
start_decrease <- which(cumsum(new_bp$lengths) >= sum(new_bp$lengths) * (gradient$start_prop))[1]

max_gradient_width <- convertUnit(width - gradient$line_width - gradient$line_width, 
    unitTo = default.units, valueOnly = TRUE)

clr_length <- which(cumsum(new_bp$lengths[end_point:1])/sum(new_bp$lengths[1:end_point]) >= 
    gradient$clr_prop)[1]
g_clrs <- colorRampPalette(colors = c(clr, gradient$clr))(clr_length)

if (start_decrease != 1) {
    # Get the part of the line that has no decrease in size
    selection <- new_bp$x < new_bp$x[start_decrease] & new_bp$x > end_points$start$x + 
        convertUnit(gradient$line_width, unitTo = default.units, valueOnly = TRUE)
    st_bp <- list(x = c(end_points$start$x + convertUnit(gradient$line_width, 
        unitTo = default.units, valueOnly = TRUE), new_bp$x[selection]), y = c(end_points$start$y, 
        new_bp$y[selection]))
    lines <- getLines(new_bp = st_bp, arrow = list(x = new_bp$x[start_decrease + 
        1], y = new_bp$y[start_decrease + 1]), width = max_gradient_width, default.units = default.units)
}

clipLinesEnd <- function(lines, no_elements_to_remove) {
    lines$top$x <- head(lines$top$x, -no_elements_to_remove)
    lines$top$y <- head(lines$top$y, -no_elements_to_remove)
    lines$bottom$x <- head(lines$bottom$x, -no_elements_to_remove)
    lines$bottom$y <- head(lines$bottom$y, -no_elements_to_remove)
    return(lines)
}
# Generate a list with all the elements
inner_gradient <- gList()
if (end_point != start_decrease) {
    getTriangleGrowth <- function(l) {
        f <- (1 - rev(cumsum(l)/sum(l)))
        return(f/max(f))
    }
    g_factor <- getTriangleGrowth(new_bp$lengths[start_decrease:end_point])

    base <- rotateWidth(x = new_bp$x[end_point], y = new_bp$y[end_point], x_origo = new_bp$x[end_point - 
        1], y_origo = new_bp$y[end_point - 1], width = max_gradient_width * 
        g_factor[1], default.units = default.units, perpendicular = TRUE)

    # Draw the top of the triangle
    gradient_pg <- polygonGrob(y = unit.c(unit(new_bp$y[end_point], default.units), 
        base$up[2], base$down[2]), x = unit.c(unit(new_bp$x[end_point], default.units), 
        base$up[1], base$down[1]), gp = gpar(fill = g_clrs[1], col = NA))

    inner_gradient <- gList(inner_gradient, gradient_pg)
    for (i in (end_point - 2):start_decrease) {
        top <- base

        base <- rotateWidth(x = new_bp$x[i + 1], y = new_bp$y[i + 1], x_origo = new_bp$x[i], 
            y_origo = new_bp$y[i], width = max_gradient_width * g_factor[end_point - 
                i], perpendicular = TRUE, prev_angle = top$angle)

        gradient_pg <- polygonGrob(y = unit.c(top$up[2], top$down[2], base$down[2], 
            base$up[2]), x = unit.c(top$up[1], top$down[1], base$down[1], base$up[1]), 
            gp = gpar(fill = ifelse(end_point - i < length(g_clrs), g_clrs[end_point - 
                i], tail(g_clrs, 1)), col = NA))
        inner_gradient <- gList(inner_gradient, gradient_pg)
    }
} else if (start_decrease != 1) {
    # Need to initiate the base just so that the rest will work
    base <- list(up = c(tail(lines$top$x, 1)[1], tail(lines$top$y, 1)[1]), down = c(tail(lines$bottom$x, 
        1)[1], tail(lines$bottom$y, 1)[1]))
    lines <- clipLinesEnd(lines, 1)
}

if (start_decrease != 1) {
    # Continue with gradient polygons if needed
    if (length(g_clrs) > end_point - start_decrease) {
        for (i in 1:(length(g_clrs) - (end_point - start_decrease))) {
            top <- base
            base <- list(up = unit(c(tail(lines$top$x, i)[1], tail(lines$top$y, 
                i)[1]), default.units), down = unit(c(tail(lines$bottom$x, i)[1], 
                tail(lines$bottom$y, i)[1]), default.units))
            gradient_pg <- polygonGrob(y = unit.c(top$up[2], top$down[2], base$down[2], 
                base$up[2]), x = unit.c(top$up[1], top$down[1], base$down[1], 
                base$up[1]), gp = gpar(fill = g_clrs[end_point - start_decrease + 
                i], col = NA))

            inner_gradient <- gList(inner_gradient, gradient_pg)

        }
    }

    if (length(lines$bottom$x) > length(g_clrs) - (end_point - start_decrease)) {
        lines <- clipLinesEnd(lines, length(g_clrs) - (end_point - start_decrease))
        gradient_pg <- polygonGrob(y = c(lines$top$y, convertY(base$up[2], unitTo = default.units, 
            valueOnly = TRUE), convertY(base$down[2], unitTo = default.units, 
            valueOnly = TRUE), rev(lines$bottom$y)), x = c(lines$top$x, convertX(base$up[1], 
            unitTo = default.units, valueOnly = TRUE), convertX(base$down[1], 
            unitTo = default.units, valueOnly = TRUE), rev(lines$bottom$x)), 
            default.units = default.units, gp = gpar(fill = gradient$clr, col = NA))
    } else {
        gradient_pg <- polygonGrob(y = c(lines$top$y[1], convertY(base$up[2], 
            unitTo = default.units, valueOnly = TRUE), convertY(base$down[2], 
            unitTo = default.units, valueOnly = TRUE), lines$bottom$y[1]), x = c(lines$top$x[1], 
            convertX(base$up[1], unitTo = default.units, valueOnly = TRUE), 
            convertX(base$down[1], unitTo = default.units, valueOnly = TRUE), 
            lines$bottom$x[1]), default.units = default.units, gp = gpar(fill = gradient$clr, 
            col = NA))
    }

    inner_gradient <- gList(inner_gradient, gradient_pg)
}

plot.new()
grid.draw(pg)
grid.draw(inner_gradient)

grid.draw(gList(pg, inner_gradient))

Phew… that's it. In the actual code I've changed the top/bottom to left/right indicating the direction of the arrow. I've also added some other stuff to make it more general. If you have some suggestions for improvements or want to help out with creating proper grobs out of the functions it would be appreciated.